Questão 174 – Geometria Plana
O fenômeno das manifestações populares de massa traz à discussão como estimar o número de pessoas presentes nesse tipo de evento. Uma metodologia usada é: no momento do ápice do evento, é feita uma foto aérea da via pública principal na área ocupada, bem como das vias afluentes que apresentem aglomerações de pessoas que acessam a via principal. A foto é sobreposta por um mapa virtual das vias, ambos na mesma escala, fazendo-se um esboço geométrico da situação. Em seguida, subdivide-se o espaço total em trechos, quantificando a densidade, da seguinte forma:
• 4 pessoas por metro quadrado, se elas estiverem andando em uma mesma direção;
• 5 pessoas por metro quadrado, se elas estiverem se movimentando sem deixar o local;
• 6 pessoas por metro quadrado, se elas estiverem paradas.
É feito, então, o cálculo do total de pessoas, considerando os diversos trechos, e desconta-se daí 1.000 pessoas para cada carro de som fotografado.
Com essa metodologia, procederam-se aos cálculos para estimar o número de participantes na manifestação cujo esboço geométrico é dado na figura. Há três trechos na via principal: MN, NO e OP, e um trecho numa via afluente da principal: QR.
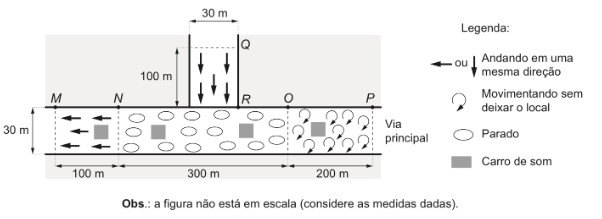
Segundo a metodologia descrita, o número estimado de pessoas presentes a essa manifestação foi igual a
A) 110.000
B) 104.000
C) 93.000
D) 92.000
E) 87.000
Solução
Separando em quatro áreas.
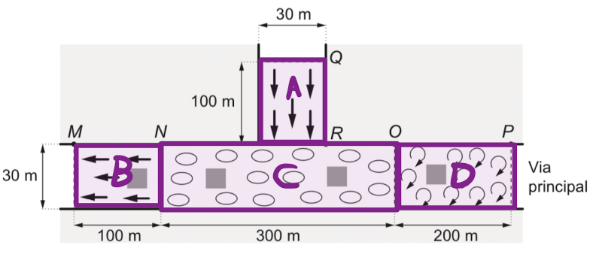
A região A é calculada por
30. 100 = 3000 m2
Nessa área se encontram pessoas andando na mesma direção, então a densidade è 4 pessoas por metro quadrado, ou seja na região A temos
3000 . 4 = 12000 pessoas
A região B tem
30 . 100 = 3000 m2
Com concentração de pessoas andando na mesma direção, 4 pessoas por metro quadrado, temos um total de
3000 . 4 = 12000 pessoas na região B
A região C tem
30 . 300 = 9000 m2
Com concentração de pessoas paradas, 6 pessoas por metro quadrado, temos um total de
9000 . 6 = 54000 pessoas na região C
A região D tem
30 . 200 = 6000 m2
Com concentração de pessoas movimentando sem deixar o local, 5 pessoas por metro quadrado, temos um total de
6000 . 5 = 30000 pessoas na região D
Foram fotografados 4 carros de som, diminuindo em 4000 a capacidade de pessoas no espaco
Somando o número de pessoas em cada região calculamos
12000 + 12000 + 54000 + 30000 – 4000 = 104000
Alternativa B
Veja a resolução com mais detalhes no vídeo abaixo!






