Questão 174 – Geometria Analítica
Uma empresa, investindo na segurança, contrata uma firma para instalar mais uma câmera de segurança no teto de uma sala. Para iniciar o serviço, o representante da empresa informa ao instalador que nessa sala já estão instaladas duas câmeras e, a terceira, deverá ser colocada de maneira a ficar equidistante destas. Além disso, ele apresenta outras duas informações:
(i) um esboço em um sistema de coordenadas cartesianas, do teto da sala, onde estão inseridas as posições das câmeras 1 e 2, conforme a figura.
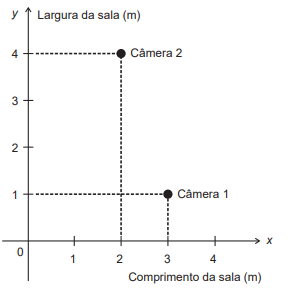
(ii) cinco relações entre as coordenadas (x ; y) da posição onde a câmera 3 deverá ser instalada.
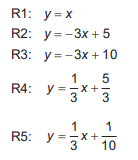
O instalador, após analisar as informações e as cinco relações, faz a opção correta dentre as relações apresentadas para instalar a terceira câmera. A relação escolhida pelo instalador foi a
A) R1.
B) R2.
C) R3.
D) R4.
E) R5
Resolução
Queremos encontrar a mediatriz da reta que é formada pelos pontos das posições das câmeras 1 e 2.
O y do ponto do meio é dado pela média das ordenadas y de cada ponto, ou seja
ym = (4 + 1)/2 = 5/2
O x também é calculado pela média, mas agora das coordenadas x de cada ponto
xm = (3 + 2)/2 = 5/2
Ou seja, queremos uma reta que passe pelo ponto (5/2,5/2)
Sabemos também que para calcular o coeficiente angular de uma reta perpendicular à outra, precisamos primeiro descobrir o coeficiente da reta referência, que é a que inclui as câmeras. Esse coeficiente é dado pela razão da diferença das ordenadas y e coordenadas x de cada ponto, ou seja
a = (1 – 4)/(3 – 2) = -3
O coeficiente da mediatriz de uma reta é -1/a, ou seja, nosso coeficiente am é
am = -1/(-3) = 1/3
Se já sabemos qual o coeficiente angular e sabemos um ponto (5/2,5/2) em que essa reta passa, conseguimos descobrir a equação inteira que é dada por
ym = am x + bm
Substituindo em x e y o par ordenado que sabemos e o valor de am temos
5/2 = (1/3)(5/2) + bm
5/2 = 5/6 + bm
5/2 – 5/6 = bm
10/6 = bm = 5/3
Então a função é
y = (1/3)x + 5/3
Alternativa D






