Uma indústria faz uma parceria com uma distribuidora de sucos para lançar no mercado dois tipos de embalagens. Para a fabricação dessas embalagens, a indústria dispõe de folhas de alumínio retangulares, de dimensões 10 cm por 20 cm. Cada uma dessas folhas é utilizada para formar a superfície lateral da embalagem, em formato de cilindro circular reto, que posteriormente recebe fundo e tampa circulares. A figura ilustra, dependendo de qual das duas extensões será utilizada como altura, as duas opções para formar a possível embalagem.
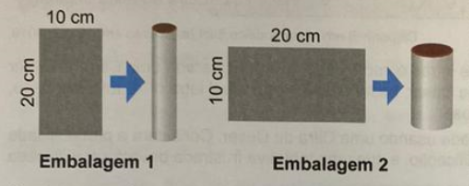
Dentre essas duas embalagens, a de maior capacidade apresentará volume, em centímetro cúbico, igual a
A) 4000π
B) 2000π
C) 4000/π
D) 1000/π
E) 500/π
Resolução
Devemos observar nessa questão que 10 cm equivale ao comprimento da circunferência que constituirá a base do cilindro de embalagem 1. Assim como, 20 cm equivale, também, ao comprimento da circunferência que constituirá a base da embalagem 2.
Sendo assim, podemos descobrir qual é o raio de cada cilindro, dessa forma:
Embalagem 1
2 x π x R = 10
R = 10 / 2 x π
R = 5 / π
Embalagem 2
2 x π x R = 20
R = 20/ 2 π
R = 10/ π
Após encontrarmos o valor do raio, podemos então calcular o volume de cada embalagem para encontrarmos qual possui a maior capacidade e qual será essa capacidade em centímetro cúbico:
Embalagem 1
V = π x R² x h
V = π x (5/ π )² x 20
v = π x 25/ π² x 20
v = 500 / π
Embalagem 2
V = π x (10/ π )² x 10
v = π x 100/ π² x 10
v = 1000 / π
Alternativa D
Veja a resolução com mais detalhes no vídeo abaixo!






