Questão 175 – Geometria Plana
No trapézio isósceles mostrado na figura a seguir, M é o ponto médio do segmento BC, e os pontos P e Q são obtidos dividindo o segmento AD em três partes iguais.
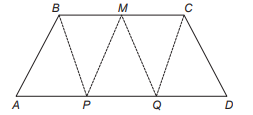
Pelos pontos B, M, C, P e Q são traçados segmentos de reta, determinando cinco triângulos internos ao trapézio, conforme a figura.
A razão entre BC e AD que determina áreas iguais para os cinco triângulos mostrados na figura é
Resolução
Podemos observar que todos os triângulos têm a mesma altura h, então se as áreas são iguais e as alturas são iguais, experimentando com dois dos triângulos usando a fórmula de área
AP.h/2 = BM.h/2
AP = BM
Ou seja, todas as partições têm tamanhos iguais que chamaremos de x.
Se BC tem duas partições
BC = 2x
E se AD te 3 partições
AD = 3x
A razão é
BC/AD = 2x/3x
BC/AD = 2/3
Alternativa B






