Os egípcios da Antiguidade criaram um sistema muito interessante para escrever números baseado em agrupamento.
O número 1 é representado pelo bastão |, o número 2 por dois bastões | | e assim por diante, até o número 9, representado por noves bastões em sequência | | | | | | | | | . A tabela a seguir representa alguns múltiplos de 10.
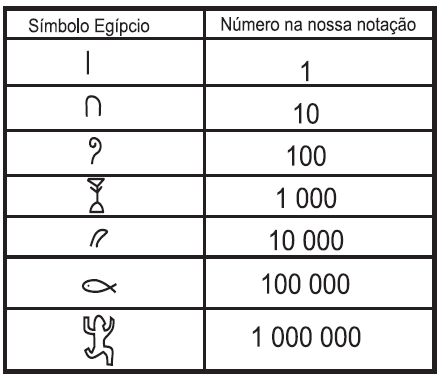
Os números de 1 a 9 999 999 na numeração egípcia derivam dos símbolos da tabela, respeitando as devidas quantidades e posições (símbolos que representam números maiores são colocados à esquerda e de maneira decrescente, são colocados os demais símbolos à direita, até a soma deles chegar ao número desejado).
Por exemplo, o numero 321 é descrito por
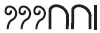
pois, 100 + 100 + 100 + 10 + 10 + 1 é igual a 321.
O número egípcio
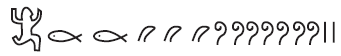
equivale ao número
A) 12 372
B) 1 230 072
C) 1 203 702
D 1 230 702
E) 1 237 200
Solução
Devemos contar a quantidade de símbolos, multiplicar pela quantidade de vezes que se repete e somar para encontrar o número
Aparece apenas um símbolo de 1 000 000
Aparece dois símbolos de 100 000 → 200 000
Aparece três símbolos de 10 000 → 30 000
Não aparece nenhum símbolo de 1000, logo não teremos valor para a casa de unidade de milhar
Aparece sete símbolos de 100 → 700
Não aparece nenhum símbolo de 10, logo não teremos valor para a casa das dezenas
Aparece dois símbolos de 1 → 2
Temos 1 230 702
Alternativa D






