Questão 176 – Geometria Plana
Uma empresa de construção comprou um terreno de formato retangular por R$ 700 000,00. O terreno tem 90 m de comprimento e 240 m de largura. O engenheiro da empresa elaborou três projetos diferentes para serem avaliados pela direção da construtora, da seguinte maneira:
Projeto 1: dividir o terreno em lotes iguais de 45 m x 10 m, sem ruas entre os lotes, e vender cada lote por R$ 23 000,00;
Projeto 2: dividir o terreno em lotes iguais de 20 m x 30 m, deixando entre lotes ruas de 10 m de largura e 240 m de comprimento, e vender cada lote por R$ 35 000,00;
Projeto 3: dividir o terreno em lotes iguais de 35 m x 20 m, deixando entre lotes ruas de 20 m de largura e 240 m de comprimento, e vender cada lote por R$ 45 000,00.
A direção da empresa decidiu dividir o terreno e utilizar o projeto que permitirá o maior lucro, sendo que este será igual ao valor obtido pela venda dos lotes, menos o valor da compra do terreno. Nesse caso, o lucro da construtora, em real, será de
A) 380 000,00.
B) 404 000,00.
C) 1 104 000,00.
D) 1 120 000,00.
E) 1 460 000,00.
Resolução
Para dividir o terreno no
Projeto 1:
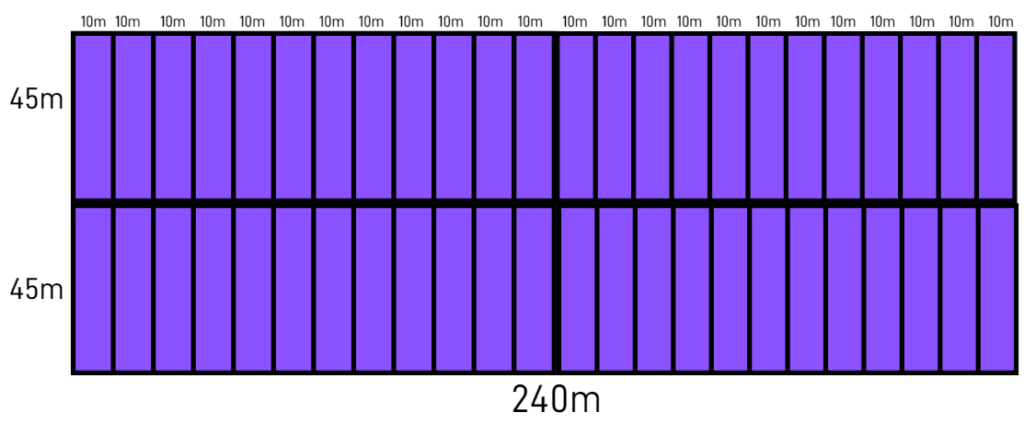
o comprimento de 90m será dividido pela dimensão de 45 m
e a largura de 240m será dividido pela dimensão 10m, assim teremos
(90/45).(240/10) = 48 lotes
Se cada um custa 23000, então a arrecadação foi de
48.23000 = 1104000 reais
Projeto 2:
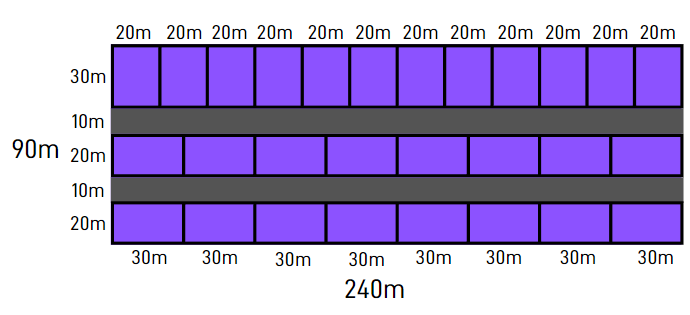
dividiremos o comprimento 90m em duas linhas de 20m e uma de 30m com ruas de 10m dividindo esses lotes.
e a largura 240m será dividida pela dimensão 30m onde o comprimento é dividido em 20m e vice e versa.
8.2 + 12.1 = 28 lotes
Cada lote custa 35000, então o total arrecadado foi
28.35000 = 980000 reais
Projeto 3:
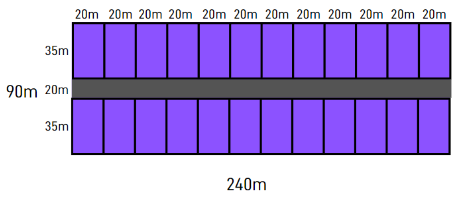
O comprimento 90 será dividido em 2 lotes de 35 m e uma rua de 20 m, enquanto a largura 240 m será dividida em 12 lotes de 20 m.
2.12 = 24 lotes
Se cada lote é 45000 reais, serão arrecadados
24.45000 = 1080000 reais
Entao o projeto 1 arrecadará mais com 1 104 000 reais, o lucro será de
1104000 – 700000 = 404 000
Alternativa B






