Certa marca de suco é vendida no mercado em embalagens tradicionais de forma cilíndrica. Relançando a marca, o fabricante pôs à venda embalagens menores, reduzindo a embalagem tradicional à terça parte de sua capacidade.
Por questões operacionais, a fábrica que fornece as embalagens manteve a mesma forma, porém reduziu à metade o valor do raio da base da embalagem tradicional na construção da nova embalagem. Para atender à solicitação de redução da capacidade, após a redução no raio, foi necessário determinar a altura da nova embalagem.
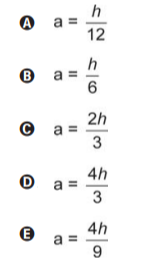
Que expressão relaciona a medida da altura da nova embalagem de suco (a) com a altura da embalagem tradicional (h)?
Solução
Chamaremos o volume inicial de V1 e o volume novo de V2, o raio inicial de r1 e o raio novo de r2 e a altura inicial de h e a nova de a.
Sabemos que
V1 = pi . r1² . h
V2 = pi . r2² . a
E que
V2 = 1/3 . V1 ou V1 = 3 . V2
r2 = r1/2 ou r1 = 2 . r2
Então, o volume inicial pode ser representado por
3V2 = pi . (2r2)². h
Isolando V2
V2 = pi . 4r2². h / 3
Relacionando o volume inicial com o novo:
V2 = pi . 4r2² . h / 3 (inicial)
V2 = pi . r2² . a (novo)
Sabemos que V2 = V2, logo
pi . 4r²2 . h / 3 = pi . r2² . a
Podemos simplificar os dois lados por pi e por r²2, o que resulta em
4h / 3 = a
Portanto,
Alternativa D






