Um tanque de armazenamento de líquidos tem o formato de uma pirâmide reta de base quadrada, cujo plano que contém essa base é paralelo a um solo plano e horizontal. Esse tanque tem capacidade de 240 litros e altura de 2 metros. Inicialmente vazio, nele é despejado um líquido à vazão constante de 0,015 m³/s.
Sabe-se que 1 L = 1 dm³ = 0,001 m³.
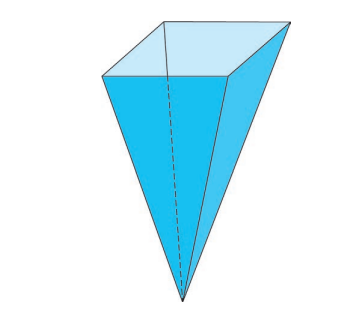
Qual expressão fornece a altura, em metro, da coluna de líquido dentro desse tanque em função do tempo t, em segundo?
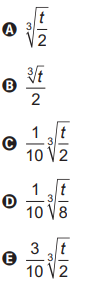
Solução
O tempo t em que o tanque será completamente cheio é
0,240 m³ / 0,015 m³ = 16 s
Sabemos também que a altura do tanque é de 2 m, podemos agora testar quais alternativas satisfazem t = 16 e h = 2.
Testando A:
h = ³√(t/2)
2 = ³√(16/2)
2 = ³√8
Verdadeiro
Testando B:
h = ³√(t)/2
2 = ³√(16)/2
2 = ³√2
Falso
Testando C:
h = (1/10).³√(t/2)
2 = (1/10).³√8
2 = 1/5
Falso
Testando D:
h = (1/10).³√(t/8)
2 = (1/10).³√(16/8)
2 = (1/10).³√2
Falso
Testando E:
h = (3/10).³√(t/2)
2 = (3/10).³√(16/2)
2 = 6/10
Falso
A única alternativa que corresponde com a realidade é a A
Alternativa A






