Segundo o Instituto Brasileiro de Geografia e Estatística (IBGE), produtos sazonais são aqueles que apresentam ciclos bem definidos de produção, consumo e preço. Resumidamente, existem épocas do ano em que a sua disponibilidade nos mercados varejistas ora é escassa, com preços elevados, ora é abundante, com preços mais baixos, o que ocorre no mês de produção máxima da safra. A partir de uma série histórica, observou-se que o preço P, em reais, do quilograma de um certo produto sazonal pode ser descrito pela função
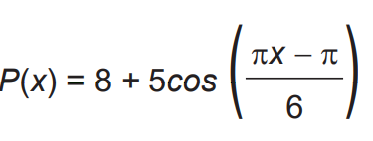
onde x representa o mês do ano, sendo x = 1 associado ao mês de janeiro, x = 2 ao mês de fevereiro, e assim sucessivamente, até x = 12 associado ao mês de dezembro.
Na safra, o mês de produção máxima desse produto é
A) janeiro.
B) abril.
C) junho.
D) julho.
E) outubro.
Solução
A produção máxima ocorre quando o preço é mais baixo.
Queremos então o momento que o cosseno atinge o seu menor valor possível para que a soma que resulta em P, seja menor.
O maior valor possível que a função cosseno pode atingir é 1 e a menor -1.
Sabemos que para o cosseno atingir o valor de -1 o ângulo deve ser de 180o, que em radianos é π
Ou seja, sendo
cos ( π.x – π / 6) = -1
Precisamos que
π.x – π / 6 = π
Resolvendo
π.x – π / 6 = π
π.x – π = 6π
Dividindo os dois lados por por π
x – 1 = 6
x = 7
O mês 7 corresponde a Julho.
Alternativa D







Tá certo!