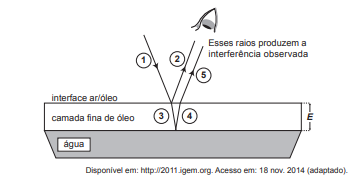
Certos tipos de superfícies na natureza podem refletir luz de forma a gerar um efeito de arco-íris. Essa característica é conhecida como iridescência e ocorre por causa do fenômeno da interferência de película fina. A figura ilustra o esquema de uma fina camada iridescente de óleo sobre uma poça d’água. Parte do feixe de luz branca incidente 1 reflete na interface ar/óleo e sofre inversão de fase 2 , o que equivale a uma mudança de meio comprimento de onda. A parte refratada do feixe 3 incide na interface óleo/água e sofre reflexão sem inversão de fase 4 . O observador indicado enxergará aquela região do filme com coloração equivalente à do comprimento de onda que sofre interferência completamente construtiva entre os raios 2 e 5 , mas essa condição só é possível para uma espessura mínima da película. Considere que o caminho percorrido em 3 e 4 corresponde ao dobro da espessura E da película de óleo
Expressa em termos do comprimento de onda (λ), a espessura mínima é igual a
A) λ/4 .
B) λ/2 .
C) 3λ/4 .
D) λ.
E) 2λ.
Solução
Para que ocorra a interferência construtiva, as ondas precisam se encontrar em fase (e não em oposição de fase). Assim, ao longo da distância 2E (ida e volta na camada de óleo de espessura E) a parte refratada do feixe (3) tem que compensar a reflexão com inversão de fase da onda 1.
2E = λ/2
E = λ/4
AlternativaA






