A aquisição de um telescópio deve levar em consideração diversos fatores, entre os quais estão o aumento angular, a resolução ou poder de separação e a magnitude limite. O aumento angular informa quantas vezes mais próximo de nós percebemos o objeto observado e é calculado como sendo a razão entre as distâncias focais da objetiva (F1) e da ocular (F2). A resolução do telescópio (P) informa o menor ângulo que deve existir entre dois pontos observados para que seja possível distingui-los. A magnitude limite (M) indica o menor brilho que um telescópio pode captar. Os valores numéricos de P e M são calculados pelas expressões: P/D = 12 e M = 7,1+5( log D), em que D é o valor numérico do diâmetro da objetiva do telescópio, expresso em centímetro.
Disponível em: www.telescopiosastronomicos.com.br. Acesso em: 13 maio 2013 (adaptado).
Ao realizar a observação de um planeta distante e de baixa luminosidade, não se obteve uma imagem nítida. Para melhorar a qualidade dessa observação, os valores de D, F1 e F2 devem ser, respectivamente,
A) aumentado, aumentado e diminuído.
B) aumentado, diminuído e aumentado.
C) aumentado, diminuído e diminuído.
D) diminuído, aumentado e aumentado.
E) diminuído, aumentado e diminuído.
Solução
A nitidez está diretamente relacionada com a resolução. Quanto menor ângulo que possibilita a distinção entre dois pontos, melhor a resolução, ou seja, maior a riqueza em detalhes da imagem observada. Essa resolução é calculada através de P =12/D e, para diminuirmos o ângulo 𝑃 devemos aumentar o valor da grandeza 𝐷, por serem inversamente proporcionais.
Ainda para melhorar a imagem, o aumento angular deve ter seu valor aumentado para aproximar a percepção do objeto observado. Uma vez que esse aumento é calculado pela razão entre F1 e F2, podemos concluir que devemos aumentar F1 e diminuir F2
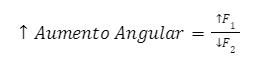
Alternativa A






